Eigenvectors
- Eigenvectors can be obtained by using eigenvalues that obtained previously.
- An eigenvector needs to be obtained for each eigenvalue.
- The following equation (The transformation equation) is used to find eigenvectors.
\[\Large
Ax = \lambda x
\]

Or the above equation can also be transformed to this equation to calculate the eigenvectors.
\[\Large
Ax = \lambda x
\]
\[\Large
Ax – \lambda x = 0
\]
\[\Large
(A – \lambda I)x = 0
\]
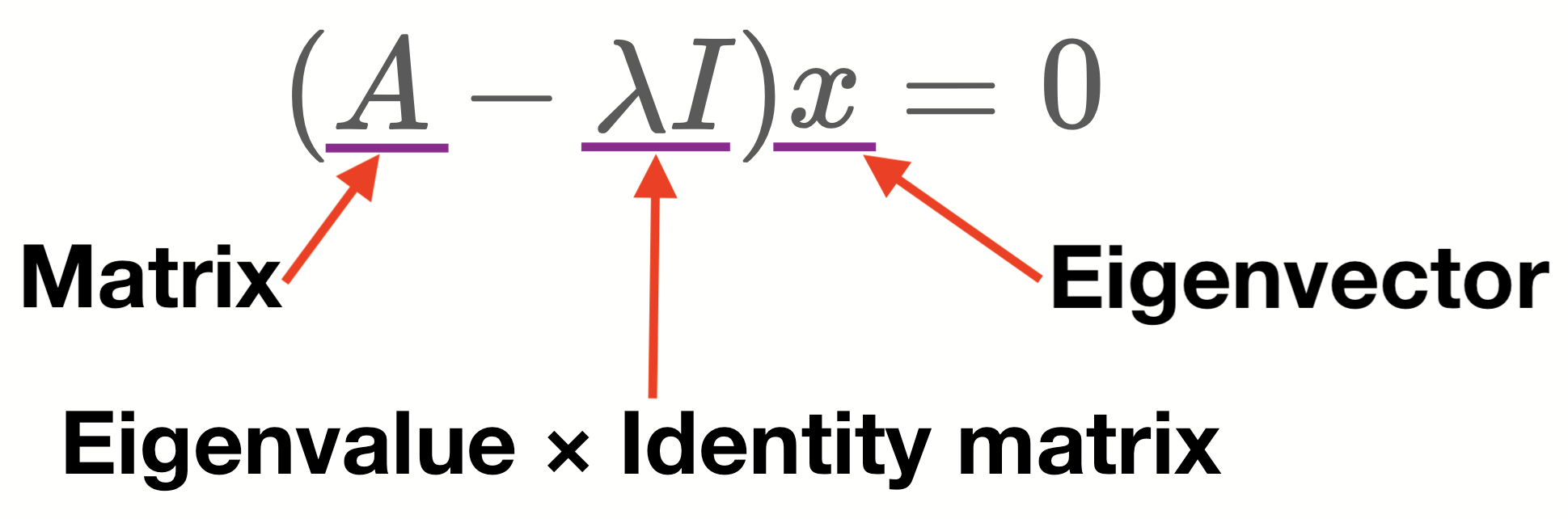
- Finding eigenvectors requires the knowledge of matrix multiplication. To learn more follow 3.2. Matrix multiplication.
\[\Large
\color{purple}{Eigenvalues,}
\]
\[\Large
\lambda_{1} = 5
\]
\[\Large
\lambda_{2} = 1
\]
- Now let’s obtain the eigenvector for each eigenvalue.
For λ1 = 5,
- Substitute A and λ to the following equation.
\[\Large
Ax = \lambda x
\]
\[\Large \begin{bmatrix} 4 & 1 \\ 3 & 2 \end{bmatrix} × \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = 5 \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large \begin{bmatrix} 4x_{1} + x_{2} \\ 3x_{1} + 2x_{2} \end{bmatrix} = \begin{bmatrix} 5x_{1} \\ 5x_{2} \end{bmatrix} \] \[\Large ↓ \] \[\Large 4x_{1} + x_{2} = 5x_{1} \] \[\Large 3x_{1} + 2x_{2} = 5x_{2} \]
\[\Large \begin{bmatrix} 4 & 1 \\ 3 & 2 \end{bmatrix} × \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = 5 \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large \begin{bmatrix} 4x_{1} + x_{2} \\ 3x_{1} + 2x_{2} \end{bmatrix} = \begin{bmatrix} 5x_{1} \\ 5x_{2} \end{bmatrix} \] \[\Large ↓ \] \[\Large 4x_{1} + x_{2} = 5x_{1} \] \[\Large 3x_{1} + 2x_{2} = 5x_{2} \]
\[\Large
4x_{1} + x_{2} = 5x_{1}
\]
\[\Large
x_{2} = x_{1}
\]
\[\Large
3x_{1} + 2x_{2} = 5x_{2}
\]
\[\Large
3x_{1} = 3x_{2}
\]
\[\Large
x_{1} = x_{2}
\]
\[\Large
x_{1} = x_{2}
\]
\[\Large x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{1} \end{bmatrix} \]
\[\Large x = \begin{bmatrix} k \\ k \end{bmatrix} \] \[\Large x_{1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \]
\[\Large x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{1} \end{bmatrix} \]
\[\Large x = \begin{bmatrix} k \\ k \end{bmatrix} \] \[\Large x_{1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \]
For λ2 = 1,
- Substitute A and λ to the following equation.
\[\Large
Ax = \lambda x
\]
\[\Large \begin{bmatrix} 4 & 1 \\ 3 & 2 \end{bmatrix} × \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = 1 \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large \begin{bmatrix} 4x_{1} + x_{2} \\ 3x_{1} + 2x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large ↓ \] \[\Large 4x_{1} + x_{2} = x_{1} \] \[\Large 3x_{1} + 2x_{2} = x_{2} \]
\[\Large \begin{bmatrix} 4 & 1 \\ 3 & 2 \end{bmatrix} × \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = 1 \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large \begin{bmatrix} 4x_{1} + x_{2} \\ 3x_{1} + 2x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \] \[\Large ↓ \] \[\Large 4x_{1} + x_{2} = x_{1} \] \[\Large 3x_{1} + 2x_{2} = x_{2} \]
\[\Large
4x_{1} + x_{2} = x_{1}
\]
\[\Large
3x_{1} = -x_{2}
\]
\[\Large
3x_{1} + 2x_{2} = x_{2}
\]
\[\Large
3x_{1} = -x_{2}
\]
\[\Large
3x_{1} = -x_{2}
\]
\[\Large x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ -3x_{1} \end{bmatrix} \]
\[\Large x = \begin{bmatrix} k \\ -3k \end{bmatrix} \] \[\Large x_{2} = \begin{bmatrix} 1 \\ -3 \end{bmatrix} \]
\[\Large x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} x_{1} \\ -3x_{1} \end{bmatrix} \]
\[\Large x = \begin{bmatrix} k \\ -3k \end{bmatrix} \] \[\Large x_{2} = \begin{bmatrix} 1 \\ -3 \end{bmatrix} \]
- So following are the eigenvectors of the above matrix ‘A’,
\[\Large
x_{1} =
\begin{bmatrix}
1 \\
1
\end{bmatrix}
~~~~~and~~~~~~
x_{2} =
\begin{bmatrix}
1 \\
-3
\end{bmatrix}
\]
Also the eigenvalues and eigenvectors of a 3 × 3 matrix can be computed in the same method.