How to calculate the determinant of a 3 × 3 matrix?
1. Select any row (or column) of the matrix
- Choose any row or column of the matrix.
Hint
It is always better to choose the row with the most number of zeros. You will understand why at the end.
- In this example we will choose the first row of the following matrix ‘A’.
\[\Large
A =
\begin{bmatrix}
2 & 1 & 4 \\
1 & 6 & 3 \\
5 & 2 & 2
\end{bmatrix}
\]
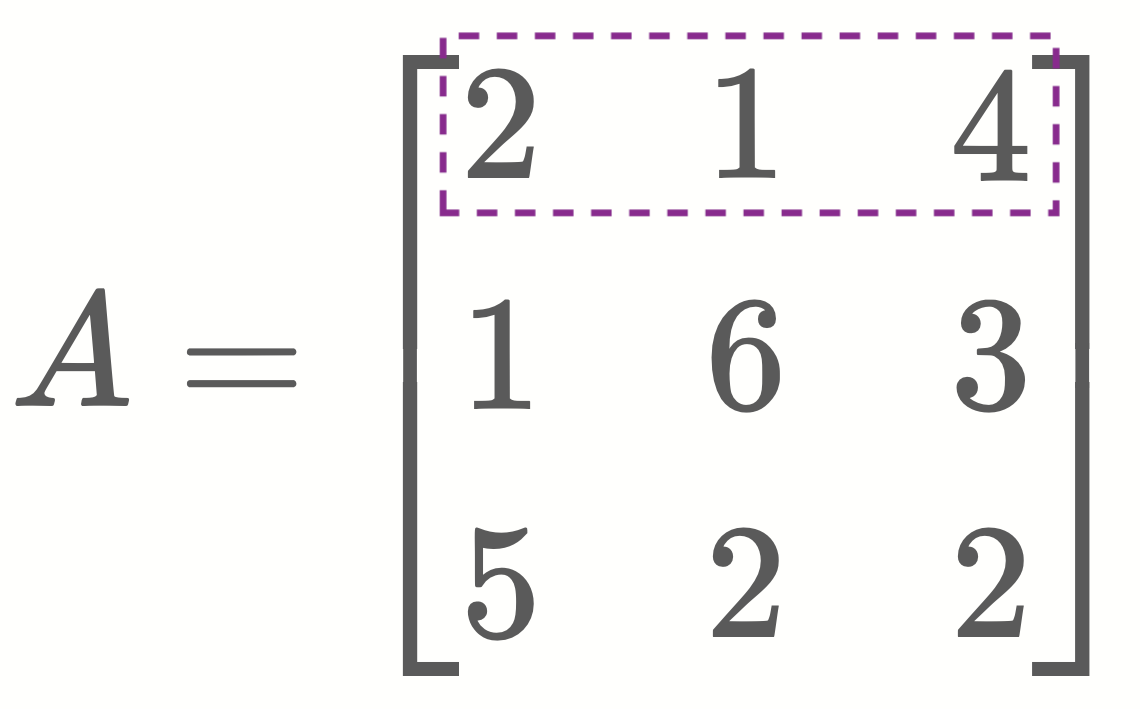
2. Find minors of all the elements in the selected row.
- In this example we need to find minors of the elements 2, 1 and 4.
- First let’s find the minor of the element ‘2’. (Minor M11)
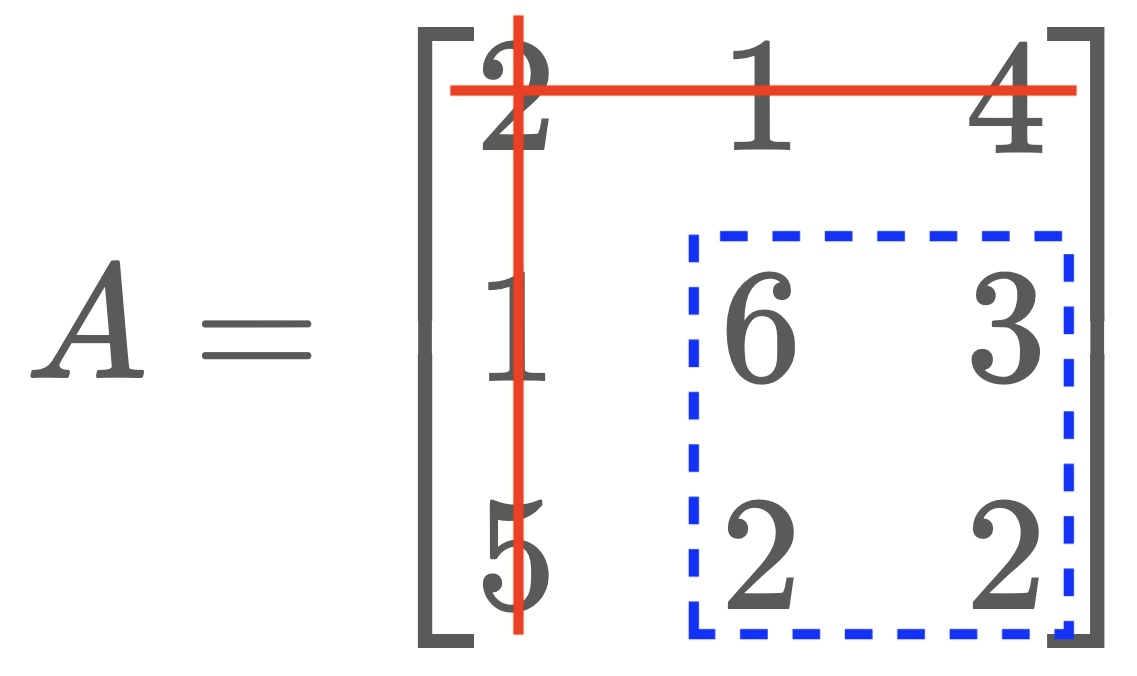
\[\Large
M_{11} =
det~
\left\vert
\begin{array}{ccc}
6 & 3 \\
2 & 2
\end{array}
\right\vert
= 6×2~-~3×2 = \mathbf{6}
\]
- Then, find the minor of the element ‘1’. (Minor M12)
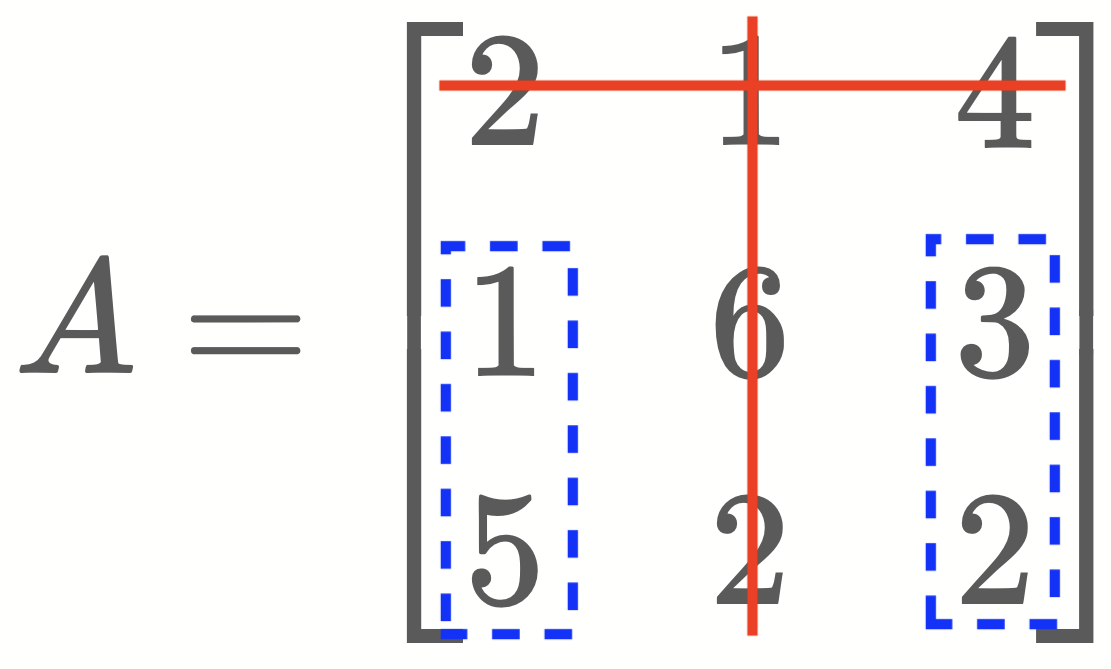
\[\Large
M_{12} =
det~
\left\vert
\begin{array}{ccc}
1 & 3 \\
5 & 2
\end{array}
\right\vert
= 1×2~-~3×5 = \mathbf{-13}
\]
- Finally, find the minor of the element ‘4’. (Minor M13)
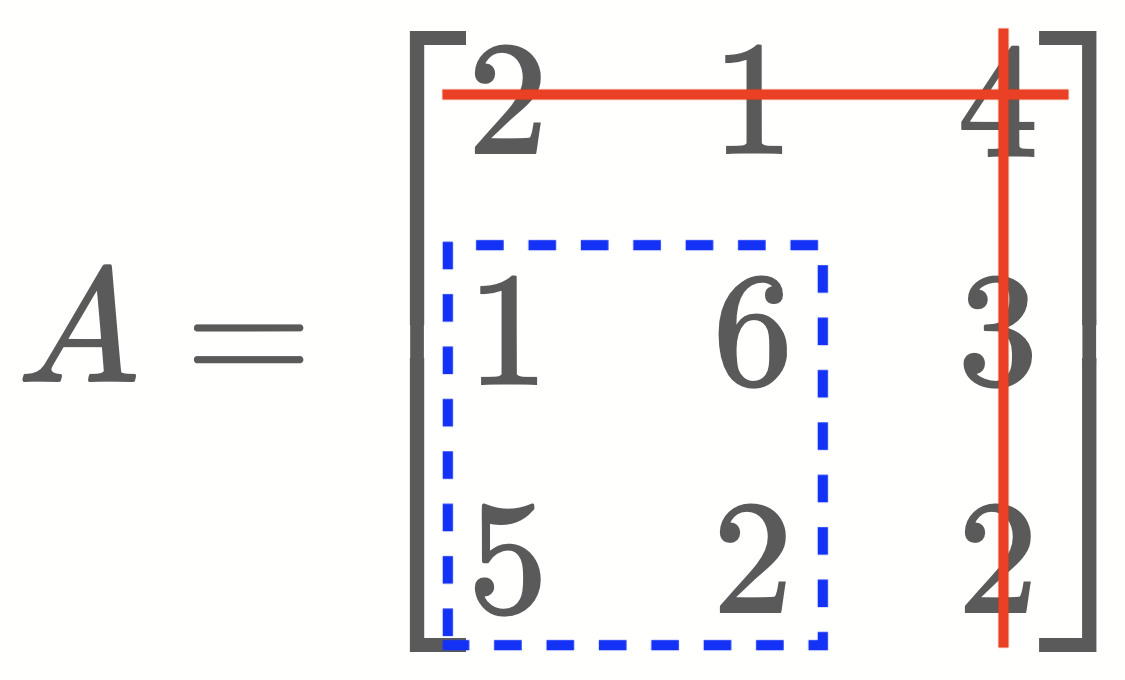
\[\Large
M_{13} =
det~
\left\vert
\begin{array}{ccc}
1 & 6 \\
5 & 2
\end{array}
\right\vert
= 1×2~-~6×5 = \mathbf{-28}
\]
3. Calculate the determinant
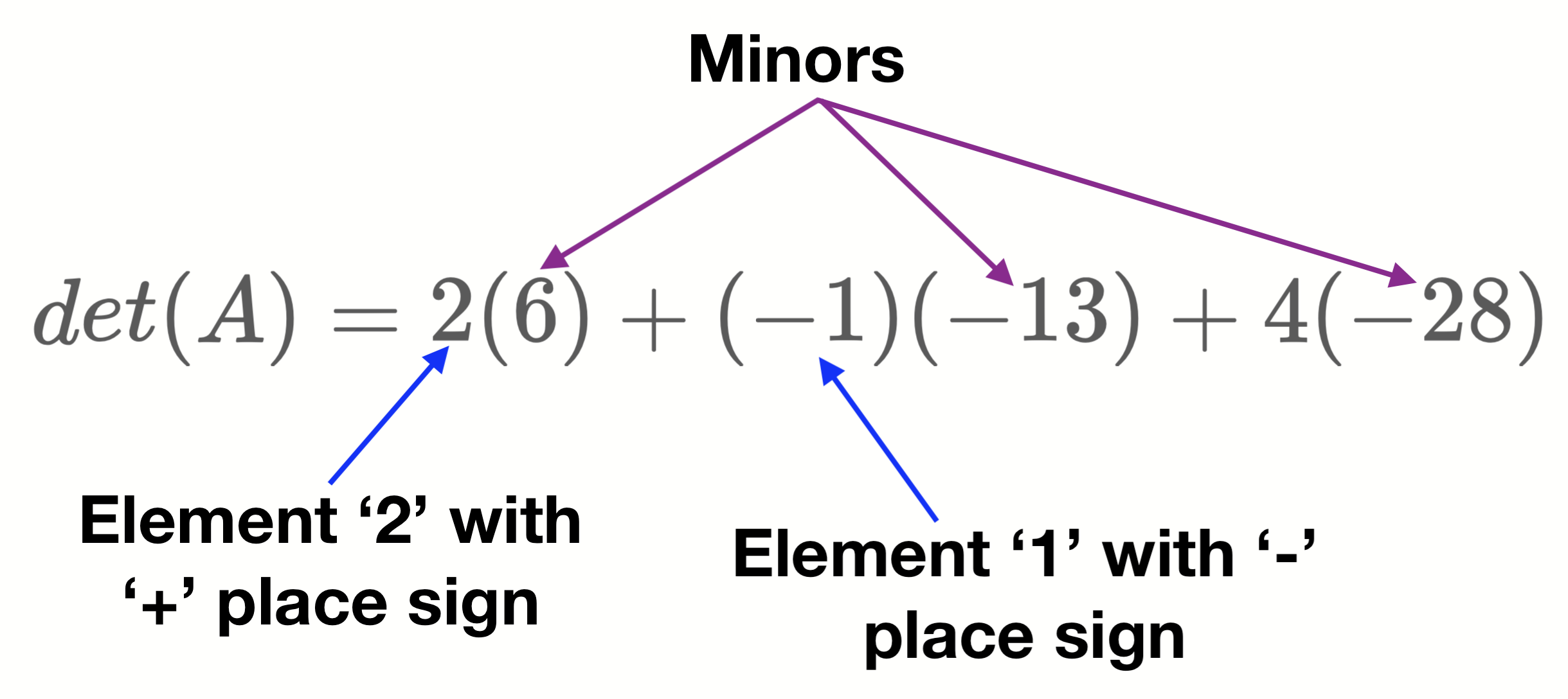
- Finally, to calculate the determinant, multiply elements with their minors with the appropriate place sign assigned to each element.
\[\Large
\begin{bmatrix}
+ & – & + \\
– & + & – \\
+ & – & +
\end{bmatrix}
\]
\[\Large
det(A) = 2(6) + (-1)(-13) + 4(-28)
\]
\[\Large
det(A) = 12 + 13 – 112
\]
\[\Large
\mathbf{det(A) = -87}
\]
- Alternatively, all the elements in the selected row can be directly multiplied with their respective cofactors to get the determinant.
Find the minor of the element “5” of the below matrix.
\[\Large
A =
\begin{bmatrix}
3&4&1\\8&8& \color{blue}{5}\\1&0&9 \end{bmatrix}
\]