Calculating the cofactor
- Cofactor is the minor of the respective element with its place sign.
- The cofactor can be calculated by simply multiplying the minor with the place sign or by using the following formula.
\[\Large
C_{ij} = (-1)^{i+j}~M_{ij}
\]
- In the above formula,
- Cij – Cofactor.
- i – Row number.
- j – Column number
- Mij – Minor
First let’s calculate the cofactor of the element ‘2’ in the first row of the following matrix using the first method.
\[\Large
A =
\begin{bmatrix}
2 & 1 & 4 \\
1 & 6 & 3 \\
5 & 2 & 2
\end{bmatrix}
\]
- First calculate the cofactor of the element ‘2’. (Minor M11)
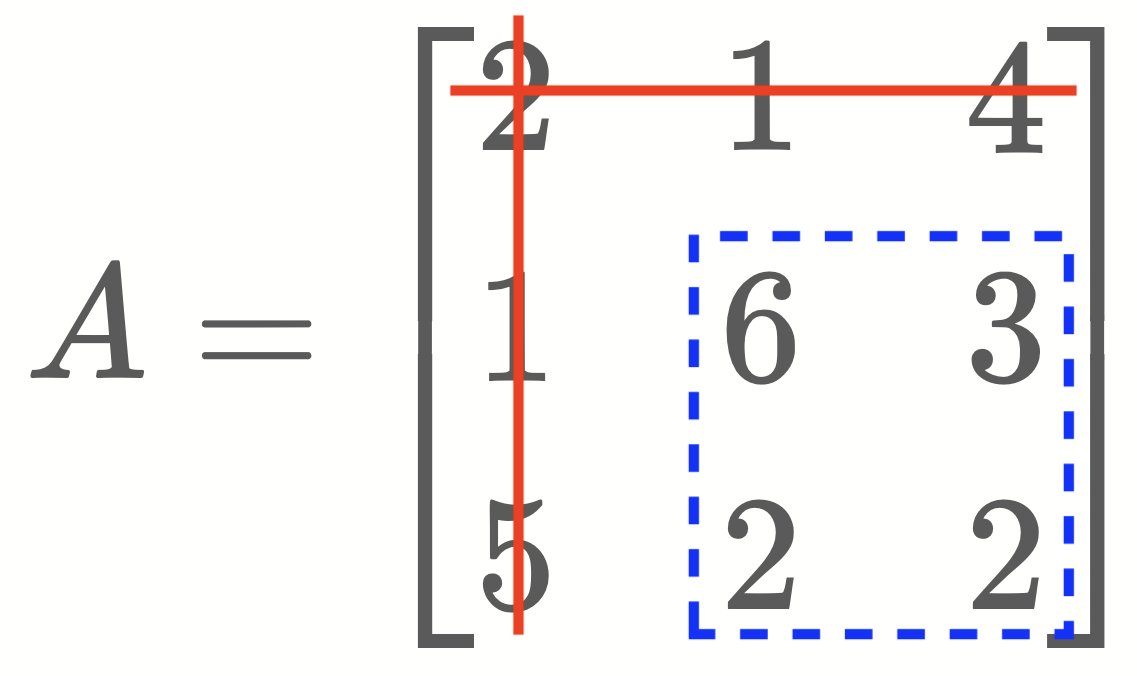
\[\Large
M_{11} =
det~
\left\vert
\begin{array}{ccc}
6 & 3 \\
2 & 2
\end{array}
\right\vert
= 6×2~-~3×2 = \mathbf{6}
\]
- Next calculate the cofactor of the above element. (Element ‘2’.)
\[\large
C_{11} = -(6)
\]
\[\large
\mathbf{
C_{11} = -6}
\]
Next let’s calculate the cofactor of the element ‘1’ of the first row using the formula.
- First calculate the minor of the element. (Minor M12)

\[\Large
M_{12} =
det~
\left\vert
\begin{array}{ccc}
1 & 3 \\
5 & 2
\end{array}
\right\vert
= 1×2~-~3×5 = \mathbf{-13}
\]
- Then substitute the values to the formula and calculate the cofactor.
\[\Large
C_{12} = (-1)^{1+2}~M_{12}
\]
\[\Large
C_{12} = (-1)^{1+2}×-13
\]
\[\Large
C_{12} = (-1)^{3}×-13
\]
\[\Large
C_{12} = -1×-13
\]
\[\Large
\mathbf{
C_{12} = 13
}\]
What is the cofactor of the element ‘3’ in the second row of the following matrix.
\[\Large
B =
\begin{bmatrix}
2&1&2\\6& \color{blue}{3}&7\\5&4&1 \end{bmatrix}
\]