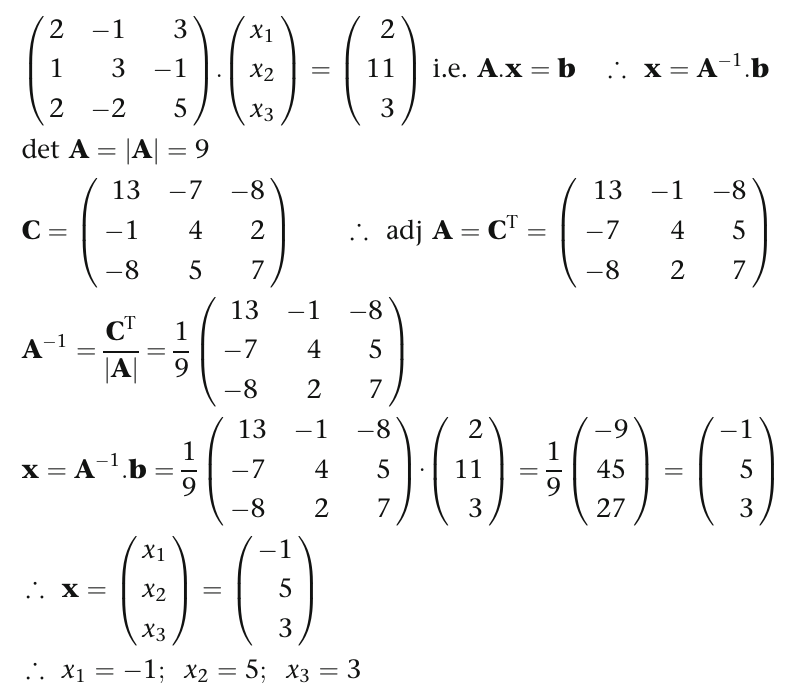Method
To solve the set of linear equations below, let’s try using this method:
\[\Large
x_{1} + 2x_{2} + x_{3} = 4
\]
\[\Large
3x_{1} + 4x_{2} + 2x_{3} = 2
\]
\[\Large
5x_{1} + 3x_{2} + 5x_{3} = -1
\]
Step 1: Write in matrix form
\[\Large
\begin{bmatrix}
1 & 2 & 1 \\
3 & -4 & -2 \\
5 & 3 & 5 \\
\end{bmatrix} ·
\begin{bmatrix}
x_{1} \\
x_{2} \\
x_{3}
\end{bmatrix} =
\begin{bmatrix}
4 \\
2 \\
-1
\end{bmatrix}
\]
\[\Large A · x = b~~~~~~~~~\therefore \ x = A^{-1} · b \]
\[\Large A · x = b~~~~~~~~~\therefore \ x = A^{-1} · b \]
Step 2: Find the inverse of A
\[\Large A^{-1} = – \frac{1}{35}
\begin{bmatrix}
-14 & 7 & 0 \\
-25 & 0 & 5 \\
29 & 7 & -10 \\
\end{bmatrix}
\]
Step 3: Solve the equations
\[\Large x=A^{-1}· b = -\frac{1}{35}
\begin{bmatrix}
-14 & 7 & 0 \\
-25 & 0 & 5 \\
29 & 7 & -10 \\
\end{bmatrix} ·
\begin{bmatrix}
4 \\
2 \\
-1
\end{bmatrix} =~~ ……..
\]
\[\Large x= -\frac{1}{35} \begin{bmatrix} -70 \\ -105 \\ 140 \\ \end{bmatrix} = \begin{bmatrix} 2\\ 3\\ -4 \end{bmatrix}
\]
\[\Large x= \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \\ -4 \end{bmatrix} ~~~~~ \]
\[\Large \therefore \ x_{1}=2;~~x_{2}=3~;~~x_{3}=-4 \]
\[\Large x= -\frac{1}{35} \begin{bmatrix} -70 \\ -105 \\ 140 \\ \end{bmatrix} = \begin{bmatrix} 2\\ 3\\ -4 \end{bmatrix}
\]
\[\Large x= \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 3 \\ -4 \end{bmatrix} ~~~~~ \]
\[\Large \therefore \ x_{1}=2;~~x_{2}=3~;~~x_{3}=-4 \]
The essential intermediate results are as follows: